Relativity visualized

A journey nearly down to the horizon of a black hole - a computer simulation renders the trip possible and shows what we should see from there.
Visualization permits journeys that the emerging space tourism will not offer for a long a time yet and maybe not at any time. One of the most interesting is the journey into the vicinity of a black hole. If we could just stay there for a while and look around, what should we see?
The destination of this virtual journey is a black hole of ten solar masses. It evolved from a much more massive star that completed its evolution with a supernova explosion, ejecting its outer layers into space while its core collapsed to a black hole. The Milky Way with its hundred billion (hundred thousand million) stars contains approximately one billion (thousand million) stellar black holes of this kind.




Our journey leads in the direction of the constellation Cygnus (Fig. 1a); in front of us we see the luminous band of the Milky Way. The computer generated pictures are computed for a horizontal camera opening angle of 90 degrees. To obtain the correct visual impression, the pictures should also be viewed with this opening angle. For a comfortable viewing distance of 30 centimetres, the individual image must then be enlarged to a width of 60 centimetres, i. e. approximately DinA2 landscape format.
We first approach the black hole up to a distance of 150 million kilometres, i. e. up to the distance of the Earth to the Sun. On our wide angle image nothing indicates the presence of the black hole (of ten solar masses, after all). Neither could it be seen with the naked eye: The region inside the horizon from which no light and no matter can escape has a circumference of only 185 kilometres and on the sky appears as a black disc with opening angle 0.2 arc seconds, far smaller than the one or two arc minute resolution of the human eye.
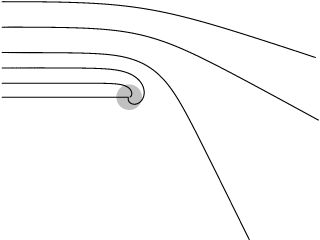
Not until we have come much closer to the black hole is the expected black disc clearly visible. Fig. 1b shows the view of the black hole from a distance of 3000 kilometres. This picture, as well as the following ones in the sequence, is taken at a constant distance from the black hole. I. e. the space ship accelerates just enough to compensate for the gravitational attraction by the black hole. The required acceleration is immense, already at this position: 15 million times the standard acceleration of gravity (g). After all, there is an object of 10 solar masses in front of us, at a distance of only half the radius of the Earth or half a percent of the solar radius.
The black disc is surrounded by a ring-like structure. From a distance of 600 kilometres (Fig. 1c, 400 million g) the structure is very clearly visible and lets a significant part of the Milky Way appear distorted. The reason for these distortions is gravitational light deflection near the black hole.
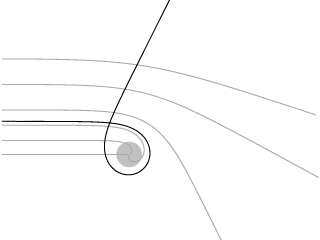
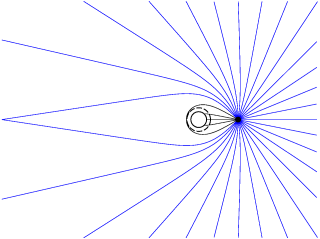
The fact that matter deflects light was one of the first tests of Albert Einstein's general theory of relativity. For a light ray that grazes the Sun, Einstein predicted a deviation by 1.75 arc seconds that has meanwhile been confirmed with high accuracy. In contrast to this minute deviation, light deflection in the vicinity of a black hole is dramatically large, as illustrated in Fig. 2: Light rays come in from the left hand side and approach a black hole (the region inside the horizon is shaded in grey). Depending on how close a light ray comes to the black hole, it will either be caught or will escape. The borderline between the two regimes is a circular orbit: light that approaches at exactly the right distance will end up circling the black hole for ever. In a small region around the circular orbit, the deflection of light rays is especially large (Fig. 2b); light circles the black hole, possibly many times, before escaping (or crossing the horizon).
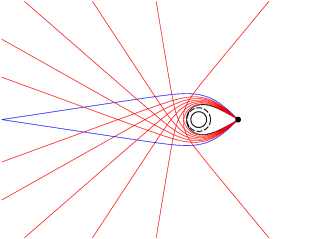
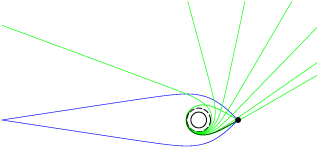
Because light rays can circle a black hole arbitrarily many times, an observer close to the black hole in principle sees the whole sky an infinite number of times. In Fig. 1c a pink ring appears around the black hole. Outside of thie ring, the whole sky is visible, inside, the whole sky is visible a second time. Fig. 3 illustrates how this comes about: Light from an object directly behind the black hole can be deflected around the black hole and so reach the observer. In the figure two such light rays are shown. Both are in the plotting plane, however, there are light rays above and below the plane that are deflected around the black hole in the same way, so that all in all the observer sees the object in the shape of a ring. The pink ring in picture 1c is generated in this way, it is the image of a gas cloud located just behind the black hole with respect to the observer.
Light seen by the observer outside the ring (Fig. 3a, blue rays) comes from all possible directions – we therefore see the whole sky without. Light rays received inside the ring (Fig. 3b, red rays), have passed closer to the black hole and have been deflected strong enough for the observer to see the upper part of the sky when looking down and vice versa. The red light rays also cover all possible directions – we therefore see the whole sky a second time, albeit inverted and distorted into a ring. In picture 1c the whole Milky Way can be made out inside the ring.
Light rays that pass even closer to the circular orbit (Fig. 3c, green rays), are deflected still more strongly. This way we see the whole sky a third time, within a narrow ring; this time seeing the upper part of the sky when looking up. The third image is such a narrow ring that it is not resolved in picture 1c. In picture 1d one can just barely see it at the rim of the black disc.
In principle infinitely many images of the whole sky are generated in this way in the form of concentric increasingly narrow rings.
Contact: Would you like to send us a message?