Relativity visualized



Wormholes are traversable connections between two universes or between two distant regions of the same universe. They are a popular feature of science fiction stories where they allow travelling to extraterrestrial cultures.
The wormholes described here are exact solutions of Einstein's field equations; they were developed by K. Thorne to give a scientific foundation to the novel Contact by C. Sagan ([1]) (The story of this development is told in [2]; [3] gives the theoretical background).
Even though these wormholes are in agreement with the theory of relativity, their implementation in practice meets a little problem: In order to curve spacetime in such a way that a wormhole forms, an exotic type of matter is required with negative energy density. In the case of the wormhole described here, the absolute values of this energy density would have to be extremely high, up to a billion times the density of a neutron star. Such a type of matter is not known in our universe. Also, to make it possible to fly and to look through the wormhole, this exotic matter must not interact with normal matter or with electromagnetic radiation.
But these technical problems cannot prevent us from simulating, on the computer, a flight through such a wormhole.
The wormhole shown here connects the place in front of the physics institutes of Tübingen University with the beautiful sand dunes near Boulogne sur Mer in the north of France (image source [4]). For the theoretical astrophysics personnel it is handy for short trips in their lunch hour.
In order to clearly show the properties of the curved space (that itself is invisible), a cubic lattice of 12 yellow rods has been built around the wormhole. The rods follow geodesics, i.e. lines that are as straight as possible. The visible distortions, especially of the rods behind the wormhole, come from light deflection in the curved space.
Eight green rods point radially inwards from the corners of the yellow cube. They approach each other and in flat space they would meet in the middle. In the curved space of the wormhole they do not.
At the throat, the interface between the two universes connected by the wormhole, the diagonal rods meet the corners of a red cube the edges of which are also geodesics. The diagonal rods continue straight-lined into the other universe. There, they move apart and meet the edges of the third, blue cube from the inside. The blue cube has the same size as the yellow one.
The following movies show a flight from Tübingen to Boulogne sur Mer and back.

The wormhole from the outside
The wormhole in front of the physics building of Tübingen University.

Approaching the throat
Approaching the throat we see the landscape on the other side of the wormhole. The green diagonal rods continue straight on.

Almost at the throat
We see that the green diagonal rods meet the corners of the blue cube from the inside.

On the other side
Looking back through the wormhole, we perceive the buildings of Tübingen University on the other side.
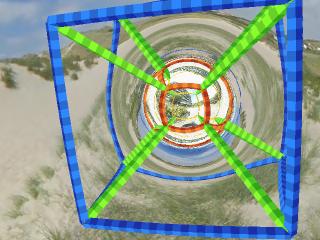
The wormhole from the outside
The wormhole is seen to hover above a sand dune near Boulogne sur Mer.

Flying back

Round trip at the throat
Before traversing the throat we turn upwards and move over the red cube that marks the plane of the throat.

Above the plane of the throat
The red cube appears to be an infinite plane. Its edges are flat and the quadratic side faces have corners of 120 degrees. "Cubes" of this kind, contradictory to everyday geometry, are possible only in a curved space.

Looking down
Through the side faces of the red cube, we can look into the other universe. Here we look down on the floor below the wormhole in Tübingen.

Looking to the side
When looking through the next red square, we see the Tübingen scene from the side.

Looking up
On to the next red square: Through it we are looking up to the sky above the wormhole.

Looking to the other side
The view through the next square shows a number of benches, upside down.

Another look downwards
We have completed the tour around the wormhole and look once again through the first red square, downwards.

Back to Tübingen
We leave the wormhole and come back to Tübingen.
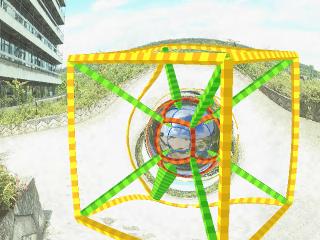
The wormhole from the outside
There, once again we look back towards the wormhole.
Morris and Thorne ([3]) describe a wormhole as a solution of Einstein's field equation with the following metric:
\[ {\mathrm d} s^2 = {\mathrm d} l^2 + (b_0^2+l^2)\,({\mathrm d}\theta^2 + \sin^2 \theta \,{\mathrm d}\phi^2) \]
\(l\) takes the values \( -\infty\ldots+\infty\). The two different signs of \(l\) represent the two universes that for large \(|l|\) are flat Minkowski spacetimes. The surface \(l = 0\) (spherical topology) links the two universes. Its surface is determined by the radius of the throat \(b_0\) .
In an orthonormal frame \( (\hat{t}, \hat{l}, \hat{\theta}, \hat{\phi}) \) , the only non-vanishing components of the Riemann tensor are
\[ R_{\hat{\theta}\hat{\phi}\hat{\theta}\hat{\phi}} = -R_{\hat{l}\hat{\theta}\hat{l}\hat{\theta}} = -R_{\hat{l}\hat{\phi}\hat{l}\hat{\phi}} = b_0^2 / (b_0^2 + l^2)^2 \]
and the components that follow from these by symmetry. Substituting the metric into the field equations we obtain the energy momentum tensor:
\[ -T^{\hat{t}\hat{t}} = -T^{\hat{l}\hat{l}} = T^{\hat{\theta}\hat{\theta}} = T^{\hat{\phi}\hat{\phi}} = 8{\mathrm \pi} \,b_0^2 / (b_0^2 + l^2)^2. \]
It has the unpleasant property of a negative energy density \( T^{\hat{t}\hat{t}} \) which according to the state-of-the-art of scientific knowledge excludes the technical realization as well as the natural occurence of such a wormhole.
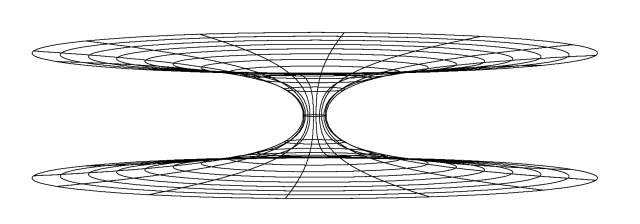
Due to the spherical symmetry one can use a two-dimensional plane through the origin to describe the main properties of the metric and the photon paths. This plane can be embedded in a three-dimensional Euclidean space. The spacelike metric in the equatorial plane reads
\[ {\mathrm d} s^2 = {\mathrm d} l^2 + (b_0^2+l^2) {\mathrm d}\phi^2. \]
With
\[ r=\sqrt{b_0^2+l^2} \]
the embedding surface (top) consists of the points with the cartesian coordinates \(x\), \(y\) and \(z\):
\[ \begin{align*} x &= r\, \cos\phi \\\ y &= r\, \sin\phi \\\ z &= b_0\, \log\left[\frac{r}{b_0} + \sqrt{\left(\frac{r}{b_0}\right)^2 - 1}\right] \cdot \left\{ \begin{array}{rl} -1 & l\lt 0 \\ 0 & l=0 \\ +1 & l \gt 0. \end{array} \right. \end{align*} \]
[1] C. Sagan, Contact, Simon and Schuster, 1985.
[2] K. Thorne, Black Holes and Time Warps: Einstein's Outrageous Legacy, W. W. Norton & Company, 1995.
[3] M. S. Morris, K. S. Thorne, Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity, Am. J. Phys. 56, 395-412, 1988.
[4]
Philippe E. Hurbain![]() ,
Panoramic photo of sand dunes near Boulogne sur Mer
in the north of France.
,
Panoramic photo of sand dunes near Boulogne sur Mer
in the north of France.
Contact: Would you like to send us a message?