Relativity visualized
Space Time Travel
|
Relativity visualized
Space Time Travel |
|
Gamow's cyclist rides at 93% of the speed of light
as can easily be inferred from the length contraction
of the wheels in Figure 1.
For the motion of a single wheel this means:
The point on the wheel momentarily
in contact with the street is at rest,
the hub moves at v=0.93c (c the speed of light)
and the point on the rim on top of the wheel moves at
0.93c with respect to the hub, i.e. with respect to the
street at
according to the relativistic velocity addition.
However, if one wants to set a wheel from rest into rotation
at nearly the speed of light, a serious mechanical problem arises:
The rim that moves in the direction of its circumference will
be length contracted, at a rim speed of v=0.93c by a factor of
.
But the motion of the spokes is perpendicular to their axes
so that the spokes are not shortened.
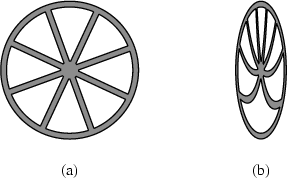
Without going into technical details we therefore equip the bicycle with wheels that are assembled in rotation. This is done in such a way that in stationary rotation the wheels have the geometric shape of ordinary wheels at rest (Figure 11a).
An ant living on the rim of the wheel would then measure a
circumference that is not
times but 8.5 times the diameter of the wheel: the intrinsic geometry
of the wheel defined in this way is not
Euclidean [9].
Add to: 
Contact: Would you like to be notified of new contributions or to send us a message?
Survey: How do you use this site and how would you like it to develop?
,
Daniel Weiskopf,
Corvin Zahn,
Date: May 25, 2002