Relativity visualized
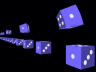
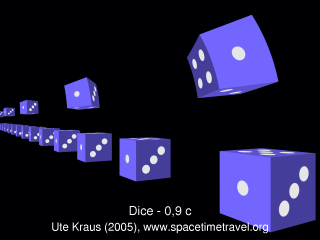
Both the sphere in Figure 2 and the cyclist in Figure 3 appear rotated. In both cases, the observer looks squarely onto the side of the object and yet gets to see its back. The apparent rotation is especially clearly visible in Figure 4. The figure shows cubes moving at 90% of the speed of light above a line of non-moving cubes. The non-moving cubes are ligned up along the path of the moving ones, and all cubes have the same orientation.
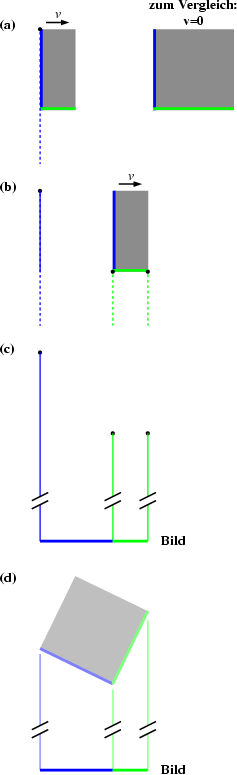
The image that we form of a moving cube is created by light rays that reach the eye at a certain instant. Since different light rays come from different points on the cube, they needed different amounts of time to reach the eye and were therefore emitted at different times. Figure 5 illustrates the consequences. We look onto the side of a moving cube. The cube is length contracted according to its velocity. Since we watch the cube from a large distance, the light rays that we receive are approximately parallel. The diagram shows three representative light rays that come from three corners of the cube. In order for all three light rays to arrive simultaneously, the light ray from the most distant corner must start first (Figure 5a). The other two must start when the first is level with the bottom edge of the cube (Figure 5b). In the meantime the cube continues to move with the result that the two light rays coming from the corners on the left hand side do not coincide so that both the left and the bottom edge of the cube are visible (Figure 5c). The same image would be created by a non-moving rotated cube of the same size (Figure 5d). Since our nonrelativistic brain is used to cubes being rotated but not to cubes moving at nearly the speed of light, we interpret the image as a rotated cube.
Contact: Would you like to send us a message?