Relativity visualized

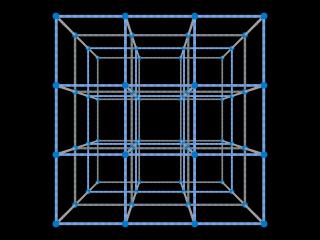
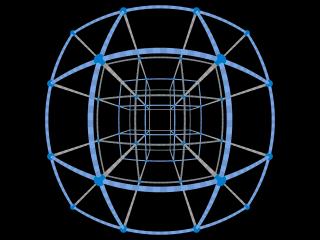

When we observe material moving at extremely high velocities in space, we always watch from a very large distance. Only in computer simulations we get the chance to watch fast moving objects nearby. Take, e.g., a cubic lattice (Fig. 9a) approaching at 90% of the speed of light (Fig. 9b). The elongation in the direction of motion is clearly visible. Equally conspicuous: the rods appear curved. Curved rods are also seen when the lattice moves away from us (Fig. 9c), appearing shortened at the same time, as expected. Thus, seen from close by, fast objects appear not only elongated, shortened or tilted, but also distorted.
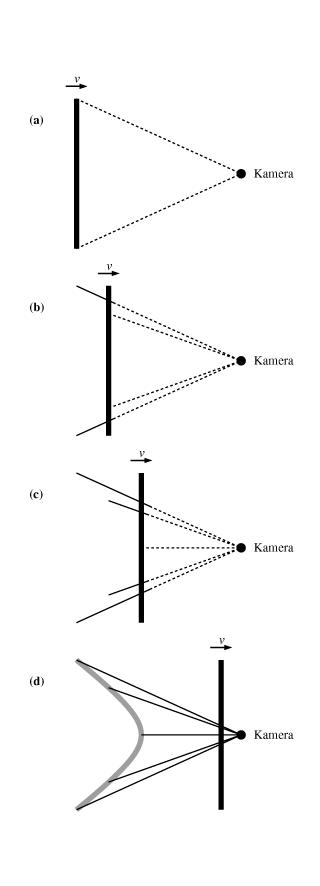
This phenomenon, as the others, is a consequence of the finite light travel times. Fig. 10 illustrates the principle for the example of a single vertical rod. The emission points of the light rays which reach the camera simultaneously, lie on a curved line. This is due to the motion of the rod and it can easily be shown that this line is in fact a hyperbola. Since any rod perpendicular to its direction of motion appears as a hyperbola, a plane perpendicular to the motion is seen in the shape of a hyperboloid. This explains the bulging shape of the lattice planes.
Contact: Would you like to send us a message?