Relativity visualized


Thinking of the rods in Figs. 1 and 2, one might be tempted to guess that any object moving at nearly the speed of light looks either elongated or shortened in the direction of motion. In fact, more surprising things happen, if the object is not, like the rods, completely flat. Fig. 5 gives an example: Cubes on a checkered platform approach us at 70% of the speed of light (left). They have the exact same orientation as the cubes at rest on the right hand side - but they appear to be tilted over to the front!
Shouldn't they appear to elongated in the same way as the moving rulers? In fact, there is no contradiction between this image and the elongated rulers. The side of the moving cube does look elongated (compare the length of the lower horizontal edge of each of the four cubes to the width of the background squares). All the same, the overall impression is that of tilted cubes, not elongated ones. This is especially true in the foreground, where the back side of the moving cube is visible, but the yellow front side is not.
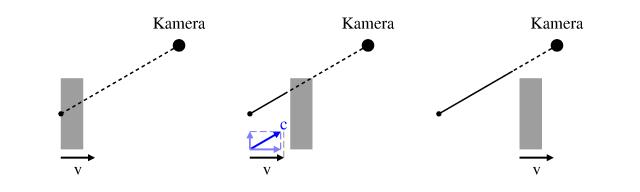
The question now is: How does light from the back side of the cube reach the camera? The cube should block the way! The answer is illustrated in Fig. 6: The cube gets out of the way fast enough. The velocity vector of a photon directed towards the camera can be split up into a horizontal component (towards the cube) and a vertical component. Each component by itself is smaller then the speed of light. The horizontal component can therefore be surpassed by the cube velocity. In this case, the cube outruns the photon, the distance between photon and cube increases while the cube moves to the right and the photon towards the camera - the photon escapes.
The reverse is true for the front side: In order for a photon to escape, its horizontal velocity component (away from the cube) must be larger than the cube's velocity. This is true only for photons which are directed not too far to the side. The directions of the escaping photons are all within a circular cone and the faster the cube, the narrower the cone. If the photons within this cone miss the camera, then the front side is not visible.
Contact: Would you like to send us a message?