Relativity visualized


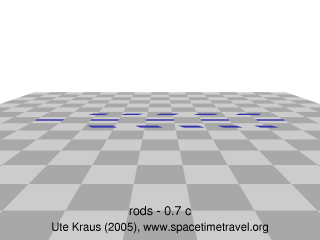
Suppose we had space ships at our disposal that could reach nearly the speed of light - would a flying space ship look shortened? Should we expect that the faster they go, the shorter they look? It turns out that things are a little more complicated. This was first pointed out by Anton Lampa in 1924 [ 1]. A computer simulation illustrates Lampa's calculations (Fig. 1): The Rulers that approach us at high speed (left, 70% of the speed of light) look much longer than the rulers that move away from us at the same velocity (right). They even look longer than the rulers at rest (middle). It must be understood that all the rulers have the same length when measured at rest, exactly the width of a square on the checquered platform. In Fig. 2 we view the same scene from the side. All moving rulers appear shortened!
In order to understand the apparent shape of the moving rulers one must examine in some detail how this image is produced. The image of any object is generated by light that comes from the object and reaches the observer's eye or camera. The light has covered the distance between the object and the camera with finite, albeit very high velocity. Since some points on the object's surface are farther away from the camera than others, the light has travelled for a longer or shorter time, depending on its point of origin.
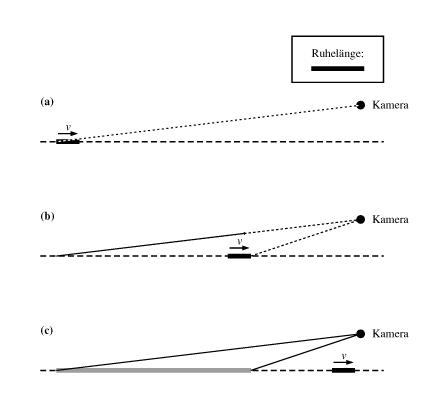
When the camera is triggered, it registers light that arrives at precisely this instant, simultaneously. This light has been emitted over a certain period, earlier or later according to its transit time. But during this period the object was in motion. Fig. 3 illustrates the consequences. Light which reaches the camera at a certain instant has been emitted by the approaching ruler over a period of time and the emission points therefore cover a region which is longer than the ruler itself; the ruler appears elongated. The elongation due to the light travel times even outweighs the relativistic length contraction: on approaching the camera, the ruler appears to be longer than at rest.
Conversely, when the ruler moves away from the camera, the light travel times let it appear shortened over and above the relativistic length contraction.
Only in the special case of motion exactly perpendicular to the line of sight, the light travel times from both ends of the ruler are the same and the length that we see is the length that we would measure. This is the case in the center of Fig. 2 as can be clearly seen by comparing the ruler length with the width of the background squares.
Contact: Would you like to send us a message?